Math
When creating parametric designs, math, especially geometry, will be your constant companion. In this short overview I will cover a few basics, which will come in handy when creating your first code-driven designs.
The circle
See circle and arc in the drawing basics.
A circle is defined by it's centre and radius. A circle's diameter is radius * 2. The circumference of the circle is Math.PI * 2 * radius. The circumference kan also be described by points located at distance radius between 0 and 360 degrees. And the surface or area of a circle is Math.PI * radius².

When you are using circles to visualise data, have in mind, that the surface of the circle increases exponentially to the radius. So do not use the radius as your scale, use the surface:
const radius = Math.sqrt(surfaceSize / Math.PI);

Radians
In many functions you will need to use radians as an input, not degrees. The conversion is quite simple: Math.PI equals 180°. So if we want to calculate the radians for a specific angle, we only need the following formula:
const rad = Math.PI / 180 * angleInDegrees;And then reverse the whole thing:
const angleInDegrees = rad * 180 / Math.PI;Polar coordinates
Our normal coordinate system is described by x, y (, z). An alternate coordinate system is the polar coordinate system. In this system, each point's location is described by radius and angle. To convert it into our normal coordinate system two simple conversions help us:
const rad = Math.PI / 180 * angle;
const x = radius * Math.cos(rad);
const y = radius * Math.sin(rad);The functions above also take negative angles (see image below for an example).
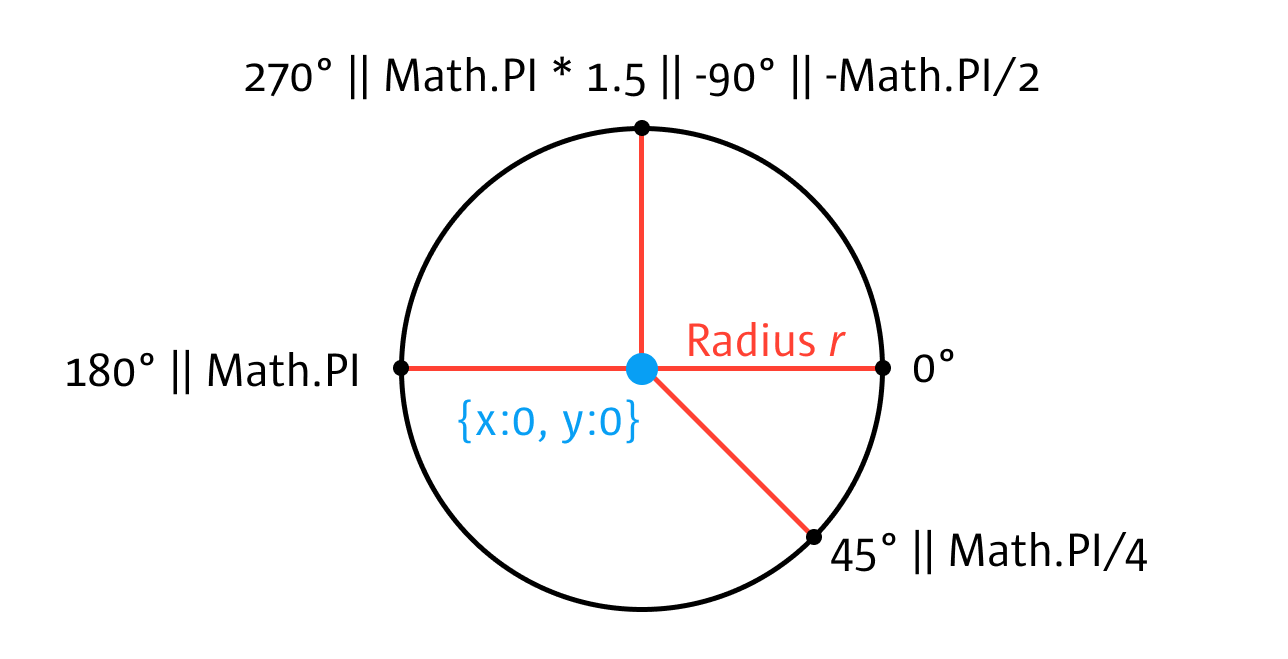
We can als do the reverse to calculate angle and radius from x, y:
const radius = Math.sqrt( x * x + y * y );
const angle = Math.atan2(y, x) * 180 / Math.PI;Distances

Some of you might remember Pythagoras and his triangle a² + b² = c². This is the basis for distance calculations in our two dimensional coordinate system:
// Point #1
const p1x = 10;
const p1y = 10;
// Point #2
const p2x = 40;
const p2y = 20;
const distX = p1x - p2x;
const distY = p1y - p2y;
const distance = Math.sqrt(
distX * distX +
distY * distY
);For short variable names, simply writing
a * ais the shortest. If you have a long variable name, there is a shorter Version:Math.pow(a, 2). This comes in even more handy when you have a higher exponent:Math.pow(a, 5).
Curves
Curves are very complex, the following examples will provide some starting points, particullarly from a parametric design perspective, rather than a mathematical/geometric perspective.
sin/cos
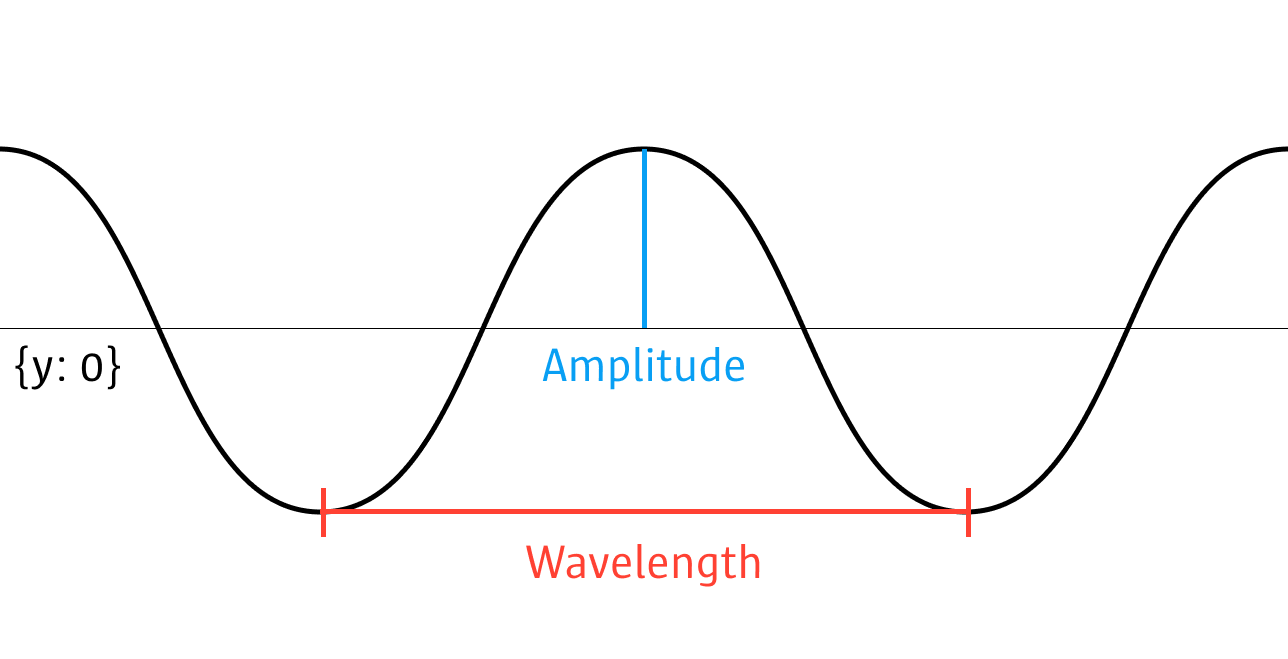
Through sin/cos we can generate waves. The problem is, the normal wavelength is Math.PI * 2 and it starts at 0. So for one wave across our sketch (sketchWidth) we would need to use the following:
const sketchHeight = 400;
const sketchWidth = 400;
beginShape();
for (let x = 0; x < sketchWidth; x += 1) {
vertex(x, sin(Math.PI * 2 / sketchWidth * x) + sketchHeight / 2);
}
endShape();But we would hardly see anything, because the amplitude is 1. But we can control the amplitude (distance between highest and lowest point):
const sketchHeight = 400;
const sketchWidth = 400;
const amplitude = 200;
beginShape();
for (let x = 0; x < sketchWidth; x += 1) {
vertex(x, sin(Math.PI * 2 / sketchWidth * x) * amplitude + sketchHeight / 2);
}
endShape();We could for example feed those two functions into our polar coordinate system:
Rule of Three
The Rule of Three is mostly of interest, if your are looking at ratios/relationships between numbers. For example we define that a rectangle with the width of 400px equals 100%. Now we want to know the width for a rectangle representing 30%. Using the rule of three we can:
const fullWidth = 400;
const fullPercentage = 100;
const searchPercentage = 30;
const searchWidth = fullWidth / fullPercentage * searchPercentage;So we require a pair defining the relationship between two scales (pixel and percentage). And from there on, we can use other values, from either scale (pixel or percentage) to calculate the corresponding value, by dividing the the pair and multiplying by the addition value, to find this value's corresponding value.
Random
The p5js function random(), allows you to set a min and max value. But sometimes you either want more control or random() is not available. Here is a quick formula to replicate the functionality:
const min = 20;
const max = 120;
const value = min + Math.random() * (max - min);
